Local system
In mathematics, local coefficients is an idea from algebraic topology, a kind of half-way stage between homology theory or cohomology theory with coefficients in the usual sense, in a fixed abelian group A, and general sheaf cohomology which, roughly speaking, allows coefficients to vary from point to point in a topological space X. Such a concept was introduced by Norman Steenrod.
Formal definition
Let X be a locally path connected topological space, and M a module over some ring R. A local coefficient system of R-modules E with fiber M is a locally trivial fiber bundle with fiber M with an action of the fundamental groupoid of the base X, that is, for each path ![\gamma�: [0,1]\to X](/2012-wikipedia_en_all_nopic_01_2012/I/6a93ee738c9209cbd6e030f37a084689.png)
, a morphism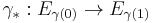 
that depends only on the homotopy class with fixed extremities of the path, is the identity on constant paths and such that composition of paths corresponds to compositions of morphisms.
In sheaf theory terms, a constant sheaf has locally constant functions as its sections. Consider instead a sheaf F, such that locally on X it is a constant sheaf. That means that in a neighbourhood of any x in X, it is isomorphic to a constant sheaf. Then F may be used as a system of local coefficients on X.
Applications
Examples arise geometrically from vector bundles with flat connections, and from topology by means of linear representations of the fundamental group.
The cohomology with local coefficients in the module corresponding to the orientation covering can be used to formulate Poincaré duality for non-orientable manifolds: see Twisted Poincaré duality.
Larger classes of sheaves are useful: for example the idea of a constructible sheaf in algebraic geometry. These turn out, approximately, to be local coefficients away from a singular set.